The calculations

At an electron beam energy of 25 GeV the mean opening angle of the photon beam (variance) amounts to 0.02 mrad. Due to this high energy the discontinuity depends very sensitive on the crystal angles 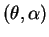$(\theta,\alpha)$which would have to be aligned to an accuracy less then half a mrad. Similarly stringent requirements apply to the electron beam specifications.

 

Table 1: Parameters used for all calculations

parameter	unit	value(s)
beam energy	MeV	25300
energy spread	MeV	20
crystal angles ( 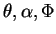$\theta,\alpha, \Phi$)	rad	0.03	0.77	0.7854
beam divergence	mrad	0.01
beam spot size	mm	1
thickness of radiator	mm	0.1
radiator temperature	K	293.17
Z of radiator (diamond,Ni)	-	6	30

In order to minimize the influence of the electron beam divergence and multiple scattering in the target, which depletes the polarisation, a 0.1 mm thick radiator was considered. The desired discontinuity at k_d=12 GeV can be achieved by only a few combinations of crystal angles. The values of tab. 1, were chosen for ease of crystal alignment. Out of a set of 9261 contributing lattice vectors (miller indices 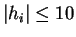$\vert h_i\vert \le 10$) the 100 strongest contributing vectors were used for this calculation. Each other vector contributes less than 10^-4 with respect to the strongest one (here the lattice vector $[02\bar 2]$) to the cross section. Including all experimental deficiencies (tab. 1), the systematic error of the polarisation prediction is estimated to about 2% absolute.

  

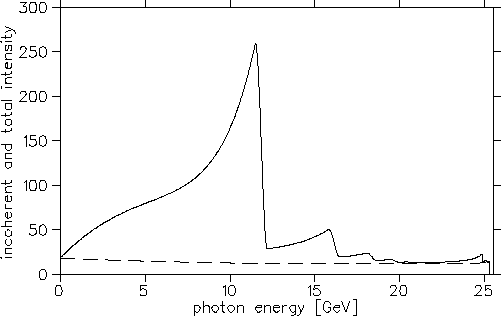
Figure: Prediction of total crystal intensity 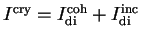$I^{\text {cry}}=I^{\text {coh}}_{\text {di}} + I^{\text {inc}}_{\text {di}}$ and incoherent 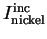$I^{\text {inc}}_{\text {nickel}}$ (dashed) photon intensity using the parameters of tab. 1 and 2, set A.