F.A. Natter
for the PiP/ToF Group of the Mainz A2 Collaboration
Physikalisches Institut, Universität Tübingen, Tübingen, Germany
The photon asymmetry measurement of 2N knock-out reactions on 4He provide new insights in the nature of correlations caused by the short distance repulsion of the NN interaction. Additionally the results show first indications of tensor correlations. A very precise description of the production of coherent bremsstrahlung will be presented which reduces systematic errors from the degree of polarisation.
The importance of short range correlations (SRC) are known for a long time [1] and their proper treatment is an indispensable ingredient in any nuclear model [2], i.e. for the binding of nuclei. The most promising way for a direct experimental confirmation is the study of photo-induced two-nucleon emission [4]. Although those experiments are challenging they have provided many empirical hints, but clear SRC effects are still not undoublty seen. The photon asymmetry plays a complementary role to the absolute cross section and represents an additional method for studying correlation in the medium [3], because it is far less subject to uncertainties with respect to FSI. One important ingredient is the precise determination of the degree of polarization, to minimize the systematic error of the asymmetry.
Linearly polarized photons are produced from electron bremsstrahlung off a crystal radiator
which provides a plane of reference for the photon polarization vector due to its regular structure [5].
Compared to an amorphous radiator this yields additional contributions which stem from a bremsstrahlung
process, when the crystal as a whole has absorbed the momentum transfer (Fig. 2 top).
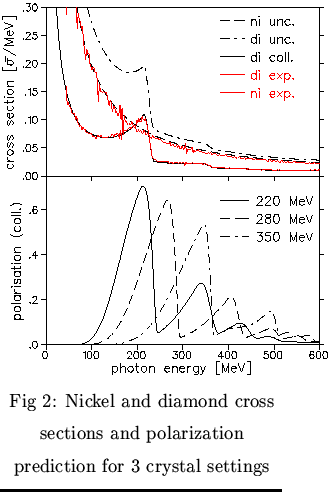
It is assumed, that the cross section and polarisation are calculated with the same precision
reproducing the experimental data equally well.
Two methods, an approximative analytical one and a Monte Carlo treatment (MCB) [5], were implemented.
The latter one is perfectly suited to cope with experimental distributions, like primary electron divergence ( ED),
multiple scattering ( MS) in the radiator and a finite beam spot size ( BS)
which decrease the degree of polarization.
Their impact is especially strong if the photon beam is collimated which in general enhances the polarization.
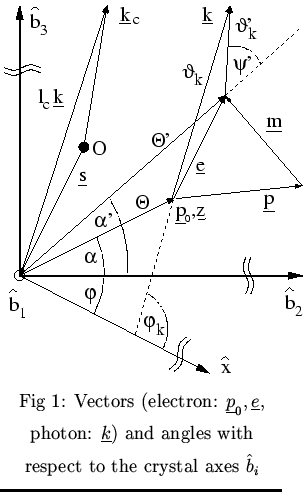
An electron which is incident at
![]() ( BS) on the radiator and has a transverse momentum
( BS) on the radiator and has a transverse momentum
![]() ( BS) is deflected by
( BS) is deflected by
![]() ( MS) due to small angle scattering
(see Fig. 1, underlined vectors denote transverse components with respect to the lattice basis vector
( MS) due to small angle scattering
(see Fig. 1, underlined vectors denote transverse components with respect to the lattice basis vector ![]() ).
The bremsstrahlung process is than calculated in the reference frame of the electron (
).
The bremsstrahlung process is than calculated in the reference frame of the electron (
![]() )
which means a transformation of the crystal orientation:
(
)
which means a transformation of the crystal orientation:
(![]() ,
,![]() )
)![]() (
(![]() ,
,![]() );
thereafter the momentum of the produced photon is retransformed:
(
);
thereafter the momentum of the produced photon is retransformed:
(![]() ,
,![]() )
)![]() (
(![]() ,
,![]() ).
Finally, the collimator condition is checked:
|
).
Finally, the collimator condition is checked:
|![]() | < rc where lc and rc denote the collimator
distance and length, resp.
With an improved description of the angle dependence of the cross section and the e-e bremsstrahlung contribution [5]
and the use of the precise MCB code, a very good agreement with the experimental spectra could be achieved,
thus reducing the systematic error of the polarization prediction to
| < rc where lc and rc denote the collimator
distance and length, resp.
With an improved description of the angle dependence of the cross section and the e-e bremsstrahlung contribution [5]
and the use of the precise MCB code, a very good agreement with the experimental spectra could be achieved,
thus reducing the systematic error of the polarization prediction to
![]() 2%.
2%.
The photon asymmetry is defined from cross sections with the reaction plane
parallel and perpendicular to the incident photon polarisation as:
![]() = -
= - ![]() WTT
WTT![]() WT =
WT = ![]()
![]()
![]() -
- ![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]() .
In the c.o.m. frame the structure function WTT has a trivial dependence on the azimuthal angle
.
In the c.o.m. frame the structure function WTT has a trivial dependence on the azimuthal angle
![]() = (
= (![]() +
+ ![]() )/2 of the reaction plane:
)/2 of the reaction plane:
![]() (
(![]() ) =
) = ![]()
![]() 1 + P
1 + P![]()
![]() cos 2
cos 2![]()
![]() ,
or i.e.
,
or i.e.
![]() =
= ![]()
![]() 1
1![]() P
P![]()
![]()
![]() =
= ![]()
![]() A.
Whereas the cross section depends only on WT which is a sum of contributions
from meson exchange (MEC), isobar (IC) and correlated one-body (C1B) currents,
the interference terms enter the asymmetry through WTT.
Therefore, the contribution from the C1B is enhanced, esp. by the interference with the IC,
leading to a high sensitivity of the asymmetry to correlations.
Furthermore, these measurements provide additional constraints to the theoretical microscopic model
and its correlation functions.
The measurement on 4He was carried out at three diamond-radiator settings corresponding to
maximal polarization at about 220, 280 and 350 MeV photon energy (Fig. 2 bottom).
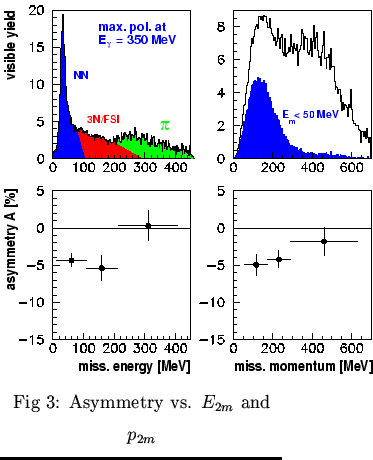
Its preliminary results (only 30% of the data) are shown in Fig. 3 and 4,
where the cross section and asymmetry is plotted versus the missing energy
E2m = E
A.
Whereas the cross section depends only on WT which is a sum of contributions
from meson exchange (MEC), isobar (IC) and correlated one-body (C1B) currents,
the interference terms enter the asymmetry through WTT.
Therefore, the contribution from the C1B is enhanced, esp. by the interference with the IC,
leading to a high sensitivity of the asymmetry to correlations.
Furthermore, these measurements provide additional constraints to the theoretical microscopic model
and its correlation functions.
The measurement on 4He was carried out at three diamond-radiator settings corresponding to
maximal polarization at about 220, 280 and 350 MeV photon energy (Fig. 2 bottom).
Its preliminary results (only 30% of the data) are shown in Fig. 3 and 4,
where the cross section and asymmetry is plotted versus the missing energy
E2m = E![]() - Tp - Tn - T rec, missing momentum
- Tp - Tn - T rec, missing momentum
![]() =
= ![]() -
- ![]() -
- ![]() and photon energy E
and photon energy E![]() , resp.
Their behaviour demonstrates, that the direct 2N absorption reveals a non-vanishing asymmetry A,
as well as 3N absorption whereas FSI, if present at all, obviously does not change the asymmetry qualitatively.
Inelastic reactions, like pion production involving very likely multi-step processes,
seem to 'forget' the photon polarisation which results in an asymmetry compatible with zero.
The contributions involved are indicated by shaded areas and stem from a calculation [6]
based on the Valencia code [2].
A cut on low E2m highly enhances direct 2N absorption which is supported by the p2m asymmetry
showing a non-vanishing value only in the momentum range of the 4He 1S state (see Fig. 3 right, black).
These events enter the energy dependend asymmetry
, resp.
Their behaviour demonstrates, that the direct 2N absorption reveals a non-vanishing asymmetry A,
as well as 3N absorption whereas FSI, if present at all, obviously does not change the asymmetry qualitatively.
Inelastic reactions, like pion production involving very likely multi-step processes,
seem to 'forget' the photon polarisation which results in an asymmetry compatible with zero.
The contributions involved are indicated by shaded areas and stem from a calculation [6]
based on the Valencia code [2].
A cut on low E2m highly enhances direct 2N absorption which is supported by the p2m asymmetry
showing a non-vanishing value only in the momentum range of the 4He 1S state (see Fig. 3 right, black).
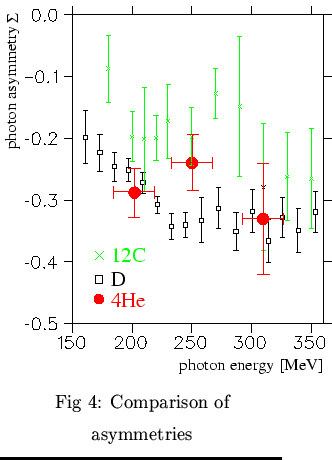
These events enter the energy dependend asymmetry
![]() (E
(E![]() ) which is plotted in Fig. 4
together with those for carbon (same experiment) and deuteron data.
The discrepancy around the
) which is plotted in Fig. 4
together with those for carbon (same experiment) and deuteron data.
The discrepancy around the ![]() resonance might be explained [3] by the interference of tensor
correlations which are not present in deuteron.
resonance might be explained [3] by the interference of tensor
correlations which are not present in deuteron.
These first results show that asymmetry measurements provide an additonal handle to investigations of SRC effects. Furthermore, they allow the conclusion that the asymmetry exhibits a high sensitivity to SRC and tensor correlations (esp. in the np channel). More stringent results can be expected from a comparison to microscopic calculations for 4He which are underway [3].
This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_navigation -split 0 -html_version 4.0,math proc.tex
The translation was initiated by Frank Natter on 1999-11-18