


Next: Results
Up: Treatment of experimental deficiencies
Previous: Monte Carlo simulation: MCB
The following approximations were used to derive an analytical function from the complicated intensity expression (eq. 4):
(i) All two dimensional transversal distributions are assumed to be Gaussian and approximated
by azimuthal symmetrical Gaussian.
(ii) A mean MS variance is used, averaged over the crystal.
(iii) A combined total electron divergence (ED) distribution
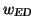 from a folding of
the MS and BD distributions is used instead.
(iv) The variation of gt, being in second order of
from a folding of
the MS and BD distributions is used instead.
(iv) The variation of gt, being in second order of
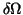 and therefore much smaller than
the variation in gl, is neglected in the intensity.
With that the uncollimated coherent intensity (eq. 4) in terms of the variation lof gl due to ED is expressed as follows:
and therefore much smaller than
the variation in gl, is neglected in the intensity.
With that the uncollimated coherent intensity (eq. 4) in terms of the variation lof gl due to ED is expressed as follows:
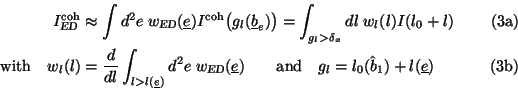
The sole dependence of the intensity on l allows the conversion of the two dimensional integral to an integral
over l in consideration of the kinematical constraint of the pancake.
Eq. 5a has to be calculated numerically but for small BD (
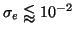 )
the integral
may be solved analytically and will be presented in a forthcoming paper.
A collimation function is derived in the following, which includes experimental deficiencies.
In the electron coordinate system the circular collimator is characterised by a lateral
displacement distribution
)
the integral
may be solved analytically and will be presented in a forthcoming paper.
A collimation function is derived in the following, which includes experimental deficiencies.
In the electron coordinate system the circular collimator is characterised by a lateral
displacement distribution
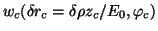 of its centre.
Due to the azimuthal asymmetry, only the integral over the displacement
of its centre.
Due to the azimuthal asymmetry, only the integral over the displacement
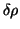 has to be calculated.
The collimator angle is now a function of the displacement and azimuthal photon angle
has to be calculated.
The collimator angle is now a function of the displacement and azimuthal photon angle
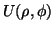 ,
which results in a convolution of the intensity[4]:
,
which results in a convolution of the intensity[4]:
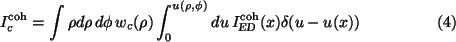
Owing to the delta function the 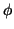 integration is trivial and the expression separates into the coherent intensity
in terms of the
integration is trivial and the expression separates into the coherent intensity
in terms of the 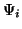 functions and a collimation function
functions and a collimation function
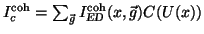 .
The treatment of collimation in the incoherent case works analogous, but the different angular dependence leads
to a remaining integral (note:
v=1/(1+Uc2):
.
The treatment of collimation in the incoherent case works analogous, but the different angular dependence leads
to a remaining integral (note:
v=1/(1+Uc2):
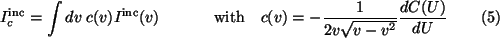
Therefore, a single collimation function accounts for experimental deficiencies in both cases
of coherent and incoherent bremsstrahlung production.
After these derivations, C(U) and c(v) have to be calculated numerically only once
and the remaining evaluation of the intensities is a closed analytical calculation providing very fast results.



Next: Results
Up: Treatment of experimental deficiencies
Previous: Monte Carlo simulation: MCB
Frank Natter
1999-07-16
![]() from a folding of
the MS and BD distributions is used instead.
(iv) The variation of gt, being in second order of
from a folding of
the MS and BD distributions is used instead.
(iv) The variation of gt, being in second order of
![]() and therefore much smaller than
the variation in gl, is neglected in the intensity.
With that the uncollimated coherent intensity (eq. 4) in terms of the variation lof gl due to ED is expressed as follows:
and therefore much smaller than
the variation in gl, is neglected in the intensity.
With that the uncollimated coherent intensity (eq. 4) in terms of the variation lof gl due to ED is expressed as follows: